Understanding Chebyshev’s Inequality: A Comprehensive Guide

Chebyshev’s Inequality is a fundamental theorem in probability theory and statistics that provides valuable insights into the distribution of data. This blog post will delve into the details of Chebyshev’s Inequality, its formulation, applications, and significance in statistical analysis.

What is Chebyshev’s Inequality?

Chebyshev’s Inequality states that for any real-valued random variable with a finite mean (μ) and finite variance (σ²), the proportion of observations that lie within k standard deviations from the mean is at least 1−1/k^2 for any k>1.

In mathematical terms, it can be expressed as:

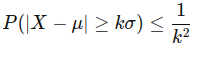
This implies that the probability of a random variable deviating from its mean by more than k standard deviations is at most 1/k^2.

Key Components of Chebyshev’s Inequality

Mean (μ):

The average value of a random variable. It provides a central point around which the data is distributed.

Variance (σ²):

A measure of how much the values of a random variable differ from the mean. A higher variance indicates that the data points are more spread out.

Standard Deviation (σ):

The square root of variance, representing the average distance of each data point from the mean.

k:

A positive integer that indicates how many standard deviations away from the mean we are considering.

Intuition Behind Chebyshev’s Inequality

The beauty of Chebyshev’s Inequality lies in its generality. Unlike other statistical rules that apply only to specific distributions (like the normal distribution), Chebyshev’s applies to all distributions with finite mean and variance. This makes it an incredibly useful tool in statistics.

For example, if you set k=2k, Chebyshev’s Inequality tells us that at least 1−1/4=75%of the data points will lie within 2 standard deviations from the mean. This can be particularly enlightening when dealing with unknown distributions.

Example of Chebyshev’s Inequality

Example – Let’s say we have a dataset representing the heights (in inches) of a group of 100 people. The mean height (μ) is 70 inches, and the standard deviation (σ) is 4 inches.

Applying Chebyshev’s Inequality

If we want to determine the minimum proportion of people whose heights fall within 2 standard deviations from the mean:

• Calculate k: Here, k=2.
• Apply the formula: According to Chebyshev’s Inequality,P(∣X−μ∣≥kσ)≤1/k^2=1/2^2=1/4​This tells us that at most 25% of the heights will be more than 8 inches away from the mean (since $2\times 4=8$).

Applications of Chebyshev’s Inequality

Quality Control:

In manufacturing, Chebyshev’s Inequality helps to determine the expected proportion of products that fall within acceptable limits based on their variability.

Finance:

Investors use this inequality to understand the risk associated with investment portfolios, assessing how much of the returns are likely to fall within a specified range.

Epidemiology:

Researchers apply Chebyshev’s Inequality to estimate the spread of diseases, helping to predict how many cases might exceed a certain threshold.

Machine Learning:

In the realm of predictive modeling, it can provide insights into model performance by assessing the distribution of errors.

Limitations of Chebyshev’s Inequality

While Chebyshev’s Inequality is powerful, it does have limitations:

Looseness:

The bounds provided by Chebyshev’s Inequality can be quite loose, especially for small values of k. For instance, it might overestimate the proportion of values within 2 standard deviations for distributions that are not heavily skewed.

Lack of Specificity:

Since the inequality applies to all distributions, it does not provide precise probabilities for specific types of distributions (e.g., normal, binomial).

Conclusion

Chebyshev’s Inequality is a cornerstone of statistical theory, offering a way to gauge the dispersion of data without making assumptions about the underlying distribution. Its applicability across various fields makes it a vital tool for statisticians and researchers alike. Understanding this inequality not only enhances your statistical acumen but also equips you with the tools necessary to analyze data effectively.

By grasping the concepts behind Chebyshev’s Inequality, you can better appreciate the behavior of random variables and make more informed decisions based on statistical analysis. Whether you’re in finance, manufacturing, or research, this theorem is invaluable for interpreting variability and risk in data.