Definition Of Student’s t-distribution

A continuous random variable X is said to have a student’s t-distribution with ν degrees of freedom if its probability density function is of the form

where ν > 0. If X has a t-distribution with ν degrees of freedom, then we denote it by writing X ∼ t(ν).

The t-distribution was discovered by W.S. Gosset (1876-1936) of Eng-land who published his work under the pseudonym of student. Therefore,this distribution is known as Student’s t-distribution. This distribution is ageneralization of the Cauchy distribution and the normal distribution. That
is, if ν = 1, then the probability density function of X becomes

which is the Cauchy distribution. Further, if ν → ∞, then

which is the probability density function of the standard normal distribution.The following figure shows the graph of t-distributions with various degrees of freedom.

 

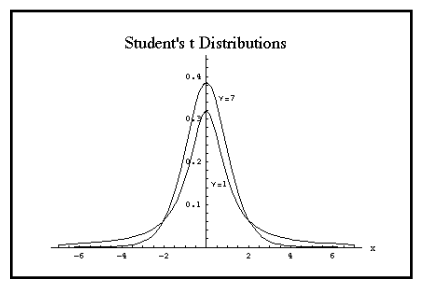
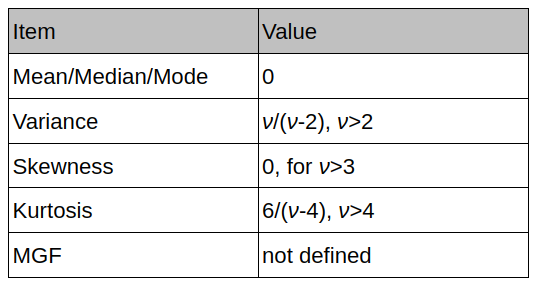
Properties of Student’s t-distribution

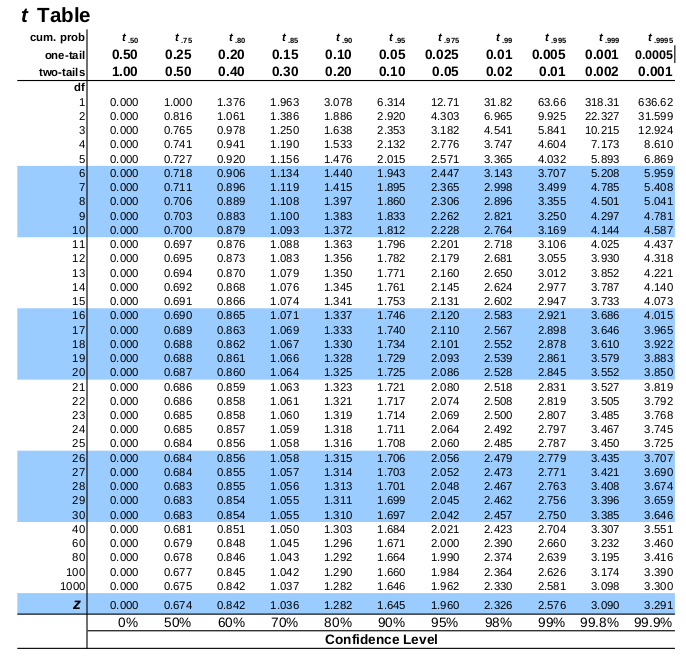
t-table:

Exercises

Example : If T ∼ t(10), then what is the probability that T is at least 2.228 ?

Answer : The probability that T is at least 2.228 is given by
P (T ≥ 2.228) = 1 − P (T < 2.228)
= 1 − 0.975  (from t − table)
= 0.025.

Example : If T ∼ t(19), then what is the value of the constant c such that P (|T | ≤ c) = 0.95 ?

Answer :                                            0.95 = P (|T | ≤ c)
= P (−c ≤ T ≤ c)
= P (T ≤ c) − 1 + P (T ≤ c)
= 2 P (T ≤ c) − 1.

Hence

P (T ≤ c) = 0.975.

Thus, using the t-table, we get for 19 degrees of freedom.

                                                                  c = 2.093.

Example : If X ∼ N (0, 1) and X1 , X2 is random sample of size two from
the population X, then what is the 75th percentile of the statistic W = ? 

Answer : Since each Xi ∼ N (0, 1), we have