Understanding Binomial Distribution :Defination , Formula , Properties and Example

Consider a fixed number n of mutually independent Bernoulli trails. Sup- pose these trials have same probability of success, say p. A random variable X is called a binomial random variable if it represents the total number of successes in n independent Bernoulli trials.

Now we determine the probability density function of a binomial random variable. Recall that the probability density function of X is defined as

f (x) = P (X = x).

Thus, to find the probability density function of X we have to find the prob-ability of x successes in n independent trails.

If we have x successes in n trails, then the probability of each n-tuple with x successes and n − x failures is

However, there are nCx  tuples with x successes and n − x failures in n trials.

Hence

Therefore, the probability density function of X is

Definition Of binomial distribution

The random variable X is called the binomial random variable with parameters p and n if its probability density function is of the form

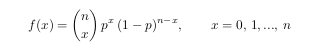
where 0 < p < 1 is the probability of success.

We will denote a binomial random variable with parameters p and n as X ∼ BIN (n, p).

Properties of binomial distribution

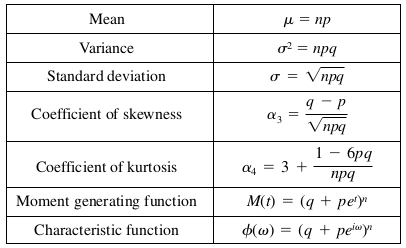
Example

Example 1 . On a five-question multiple-choice test there are five possible answers, of which one is correct. If a student guesses randomly and indepen-dently, what is the probability that she is correct only on questions 1 and 4?

Answer : Here the probability of success is p = 1/5 , and thus 1 − p = 4/5 .Therefore, the probability that she is correct on questions 1 and 4 is

P (correct on questions 1 and 4) =p^2 (1 − p)^3

= (1/5)^2 . (4/5)^3

= 64/5 = 0.02048.

Example 2. Example 5.4. On a five-question multiple-choice test there are five possible
answers, of which one is correct. If a student guesses randomly and indepen-
dently, what is the probability that she is correct only on two questions?

Answer : Answer: Here the probability of success is p = 1/5 , and thus 1 − p = 4/5 . There
are 5C2 (5 choose 2) different ways she can be correct on two questions. Therefore, the
probability that she is correct on two questions is

P (correct on two questions) = 5C2 P^2 (1- P)^3

= 10 (1/5)^2 (4/5)^3

= 640/5^5 = 0.2048

 

Example 3. What is the probability of rolling two sixes and three nonsixes in 5 independent casts of a fair die

Answer: Let the random variable X denote the number of sixes in 5 in-dependent casts of a fair die. Then X is a binomial random variable with probability of success p and n = 5.The probability of getting a six is p = 16 .

Hence

P (X = 2) = f (2) = 5C2 (1/6)^2 (5/6)^3

=  10 (1/36) (125/216)

=  1250/7776 = 0.160751.