Understanding the Central Limit Theorem: A Key Concept in Statistics

The Central Limit Theorem (CLT) is a fundamental principle in statistics that has profound implications for data analysis and probability theory. Whether you’re a student, researcher, or business analyst, understanding the CLT can enhance your ability to interpret data effectively.

What is the Central Limit Theorem?

The Central Limit Theorem states that when you take a large enough sample size from a population, the sampling distribution of the sample mean will be approximately normally distributed, regardless of the population’s original distribution. This holds true as long as the samples are independent and identically distributed (i.i.d.).

The Formula of the Central Limit Theorem

The formula to understand the behavior of the sample mean x̄ is expressed as:

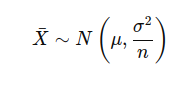
Where:

• x̄ is the sample mean.
• N denotes a normal distribution.
• μ is the population mean.
• σ^2 is the population variance.
• n is the sample size.

This means that as the sample size $n$ increases, the distribution of the sample mean  approaches x̄ a normal distribution with mean μ and variance σ^2/n . 

Why is the Central Limit Theorem Important?

Simplifies Analysis:

The CLT allows statisticians to make inferences about population parameters even when the population distribution is unknown. By relying on the normal distribution, researchers can use various statistical methods that assume normality.

Applicability:

The theorem applies to a wide range of fields, including economics, psychology, and quality control. This universality makes it a cornerstone of inferential statistics.

Foundation for Hypothesis Testing:

Many statistical tests, such as t-tests and ANOVAs, are based on the assumption of normality. The CLT justifies this assumption, making these tests reliable tools for hypothesis testing.

How Does the Central Limit Theorem Work?

To illustrate the CLT, let’s consider a practical example:

Population:

Imagine a population of students with varying heights. The height distribution might be skewed or uneven.

Sampling:

If you take random samples of 30 students and calculate the mean height of each sample, you’ll create a new distribution of sample means.

Result:

According to the CLT, as you continue to take larger samples (30 or more), the distribution of these sample means will begin to resemble a normal distribution, even if the original population distribution was not normal.

Practical Implications of the Central Limit Theorem

Quality Control:

In manufacturing, businesses can assess product quality by examining sample means rather than measuring every item. The CLT ensures that sample means will follow a predictable pattern.

Polls and Surveys:

Pollsters rely on the CLT to infer the opinions of a large population from a relatively small sample. This helps in making accurate predictions in elections and market research.

Finance and Economics:

Analysts use the CLT to model returns on investments and to understand market behaviors, enabling better decision-making.

Conclusion

The Central Limit Theorem is a powerful concept that forms the backbone of statistical analysis. By allowing statisticians to work with sample means, the CLT provides a pathway to understanding larger populations through smaller, manageable datasets. Whether you’re analyzing data for academic research or making informed business decisions, grasping the CLT is essential for effective data interpretation.