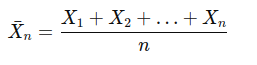Understanding the Law of Large Numbers: A Comprehensive Guide

The Law of Large Numbers (LLN) is a fundamental concept in probability and statistics that plays a crucial role in various fields, from finance to insurance and beyond. This principle explains how the average of a large number of trials tends to get closer to the expected value as the number of trials increases. In this article, we will delve into the different types of LLN, its mathematical foundation, practical applications, and some common misconceptions, along with illustrative examples.

 What is the Law of Large Numbers?

The Law of Large Numbers states that as the size of a sample increases, the sample mean will converge to the expected value (or population mean). Simply put, the more times an experiment is conducted, the more likely the average of the results will reflect the true average of the entire population.

Types of Law of Large Numbers

There are two primary forms of the Law of Large Numbers: the Weak Law and the Strong Law.

Weak Law of Large Numbers:

This version states that for any small positive number (epsilon), the probability that the sample average deviates from the expected value by more than epsilon approaches zero as the sample size approaches infinity. This means that, with a large enough sample size, the average will be very close to the expected average.

Strong Law of Large Numbers:

This stronger version asserts that the sample averages will almost surely converge to the expected value as the number of trials goes to infinity. In this case, the average will equal the expected value with a probability of 1 in the limit of an infinite number of trials.

Mathematical Representation of the Law of Large Numbers

To better understand the Law of Large Numbers, let’s consider a random variable X with an expected value E[X]=μ. Suppose we have a series of independent and identically distributed (i.i.d.) random variables X1,X2,X3,…,Xn. The sample mean X̅n is defined as:

​​

According to the Weak Law of Large Numbers, for any ϵ>0:

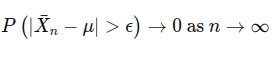
The Strong Law of Large Numbers states that:

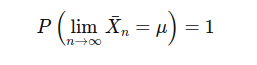
Practical Implications of the Law of Large Numbers

The Law of Large Numbers has significant implications across various sectors:

1. Insurance

Insurance companies rely on the LLN to predict payouts accurately. By pooling a large number of policies, they can estimate average claims and set premiums accordingly, ensuring profitability.

Example: If an insurance company covers 10,000 car insurance policies, it can estimate that, on average, claims will amount to $2,000 per policy. If it calculates the average claim from a smaller sample, it might fluctuate. However, as they assess more policies, they can confidently approach the expected average of $2,000.

2. Finance and Investing

Investors use the LLN to make informed decisions based on historical data. For instance, they assume that over a large number of trades, the average return will align with expected market returns.

Example: A mutual fund manager analyzes the returns of 1,000 different stocks. While individual stock performance may vary greatly, the average return of all stocks will converge toward the expected market return over time.

3. Quality Control in Manufacturing

In manufacturing, companies use large samples to assess the quality of their products. By analyzing a substantial number of items, they can ensure that the average quality meets standards.

Example: A factory producing light bulbs may test 1,000 bulbs for brightness. While some bulbs might be dimmer than expected, the average brightness of the 1,000 tested will closely reflect the average brightness of all bulbs produced.

4. Polling and Market Research

Pollsters and market researchers utilize the LLN to ensure that their sample results accurately reflect the views or behaviors of the larger population. Larger sample sizes lead to more reliable data.

Example: If a political poll surveys 1,000 voters, the results can provide a solid estimate of the candidate’s support. However, a survey of just 100 voters may yield a skewed result, potentially misrepresenting the overall voter sentiment.

Common Misconceptions About the Law of Large Numbers

While the Law of Large Numbers is a powerful tool, it’s important to clarify some common misconceptions:

1. The Gambler’s Fallacy

One prevalent misunderstanding is the gambler’s fallacy, where individuals believe that past outcomes affect future probabilities in independent events. For example, if a coin has landed heads five times in a row, one might incorrectly assume tails is “due” to occur.

2. Small Sample Sizes

The LLN applies as sample sizes approach infinity. Smaller samples can still show significant variations from the expected average, leading to unreliable conclusions.

3. Independence of Trials

The LLN assumes that the samples are independent. If the outcomes are correlated, the LLN may not hold, and averages may not converge to the expected value as expected.

Conclusion

The Law of Large Numbers is a foundational principle in probability and statistics, emphasizing the importance of large sample sizes in obtaining reliable estimates. Its applications span various fields, making it essential for anyone involved in data analysis, finance, insurance, or quality control. By understanding the LLN and its implications, one can make more informed decisions based on statistical data. Whether you’re an investor, a researcher, or simply curious about how averages work, grasping the Law of Large Numbers is crucial for interpreting data accurately.